矩阵论中的“dim”到底是什么鬼?
PS:89游戏提供三国游戏/真人恋爱/绅士游戏/3A单机游戏大全,点我立即前往》》》绅士游戏下载专区
兄弟们!老司机带你们玩转矩阵论,今天咱们就来揭秘一下这个神秘的“dim”!
你得知道,这“dim”可不是什么暗淡无光的意思,它可是矩阵论中的一个大人物——维度!
“维度”听着有点抽象,其实简单来说,就是用来描述空间大小的。比如,我们生活在三维空间,可以上下左右前后移动,但二维空间的生物只能在平面上活动,一维空间的生物就只能像蚂蚁一样沿着一条直线爬行。
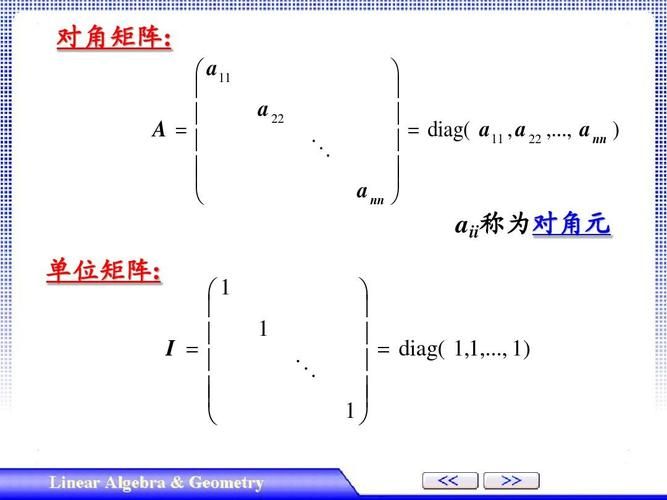
在矩阵论里,我们用“dim”来表示一个向量空间的维度。
向量空间?什么玩意儿?

别慌,别慌,这其实就是一群向量的集合。想象一下,你用一个箭头来表示一个向量,把一堆这样的箭头放在一起,就构成了一个向量空间。
举个例子,二维平面上的所有向量就构成一个二维向量空间,因为你可以用两个方向来表示一个向量,就像你用“东经X度,北纬Y度”来描述一个地球上的位置一样。
“dim”到底怎么用?
简单来说,一个向量空间的“dim”就是用来表示这个空间中需要多少个独立向量才能表示所有向量。
什么意思呢?
想象你有一个二维平面,你可以用两个相互垂直的向量(比如横轴方向和纵轴方向)来表示平面上的任何一个向量。所以,二维平面的“dim”就是2。
而三维空间需要三个相互垂直的向量才能表示空间中的任何一个向量,所以三维空间的“dim”就是3。
“dim”还有其他含义?
当然!在高等代数中,除了用来表示向量空间的维度之外,“dim”还可以表示线性无关向量个数,也就是用来表示一个线性空间的基底的个数。
说白了,就是用最少的向量来描述整个空间,就像用两个相互垂直的向量来描述二维平面一样。
“dim”的重要性?
“dim”是矩阵论和线性代数中的一个重要概念,它可以帮助我们理解向量空间的结构,并进行各种运算。
例如,通过“dim”,我们可以判断两个向量空间是否同构,也就是判断它们是否可以互相转化。
总结
简单来说,“dim”就是一个用来描述空间大小的工具,它可以帮助我们理解向量空间的结构和性质。
别看“dim”长得简单,它在数学领域可是大有用途呢!
你现在对“dim”了解多少了?你还有哪些关于矩阵论或者线性代数的惑?快来留言分享你的想法吧!